学习博弈论，从入门、进阶到精通，如何列书单？

发布时间：

2023-08-24 12:34

阅读量：

刚刚完成了博弈论的入门，腆着脸来分享一下自己的经验。

我始终认为，单纯磕书不如找名校的课程视频，所以，首推耶鲁大学的博弈论课程。

【公开课】耶鲁大学：博弈论（中英双语字幕）_哔哩哔哩_bilibili

其次推荐的是书本，给执意要看书的人们，不妨就按照耶鲁大学Benjamin Polak老师的推荐来，星星数量代表难度。

Dutta. Strategy and Games ⭐

Joel Watson. Strategies ⭐⭐

Avinash Dixit. Thinking Strategically ⭐⭐⭐

最后，厚着脸皮推荐一下自己写的课程心得，也可以作为博弈论入门的良好学习材料。因为写的时候是打算将来自己开选修课做教案用的，所以给自己的要求是写的让零基础的同学也能看懂。全文都按照Benjamin Polak的课程逻辑和顺序进行了细致的梳理，全部转化为了中文，每个章节和案例都有完整的图示推导，希望能得到同好们的认可。

刘显文：执剑者的自我修养——博弈论课程心得

以下为全文。

前言：

寒假在家，拥有了一整段闲暇的时光，遂把收藏已久的耶鲁大学公开课：博弈论进行了完整的学习，特作此文，以为留念。

之所以起这个标题，一方面是蹭蹭最近的三体热度，毕竟作为一个科幻世界时代追过来的老粉，还是很开心看到电工的作品如今可以广为流通。但另一方面，作为一个社会科学人，又很是遗憾，毕竟在这么伟大的科幻作品里，当代社会科学没能捞到什么出场的机会。不知道哪一天能有一部描述未来的作品，能够在社会组织结构、社会文化、心理学、经济学等方面有突破性的描写。

话说回来，如果执剑人在竞选前都强制要求修习博弈论课程并结业，不知道程心会不会表现得靠谱一点（笑）。

本门课程的授课老师是Benjamin Polak，英国人，经常自嘲上课时带着奇怪的口音，并拥有制作谜一般的板书的能力。

从履历上看，Benjamin是妥妥的英美系学霸，84年学士毕业于剑桥，85年硕士毕业于西北大学，92年博士毕业于哈佛，视频录制时的07年秋天已是耶鲁大学的讲师。有趣的是，在课程中，Benjamin偶尔会玩的梗除了英美差异、师生年龄差异，还有对哈佛的各类调侃，想来对于自己的博士岁月甚是“怀念”。

此处附上耶鲁大学对Benjamin Polak的官方介绍：

Professor Polak is an expert on decision theory, game theory, and economic history. His work explores economic agents whose goals are richer than those captured in traditional models. His work on game theory ranges from foundational theoretical work on common knowledge, to applied topics in corporate finance and law and economics. Most recently, he has made contributions to the theory of repeated games with asymmetric information. Other research interests include economic inequality and individuals' responses to uncertainty. Professor Polak is currently engaged in an ambitious empirical project that tackles questions of industrial organization in the setting of industrial revolution in England.

为了行文方便，接下来我就简称老师为Ben。

1. 囚徒困境 Prisoner's Dilemma

开篇介绍，Ben首先提出，博弈论是一种研究策略形势的方法，以经济学中的情形举例说明，完全竞争市场上只能被动接受均衡价格的企业以及垄断市场上超级寡头企业都不处在一个策略形势之中，介于完全竞争和完全垄断之间的，既不完全竞争，此时参与者们就会需要面对策略形势了。

此外，策略形势下参与者受到的影响是取决于行动的，不仅仅指参与者本人的行动，也取决于其他参与者的行动。

目前，博弈论这种分析方式被广泛的应用到了经济学、政治学、法学、生物学、体育等各个方面。

然后，Ben推荐了几本课程参考书目：

Dutta. Strategy and Games ⭐

Joel Watson. Strategies ⭐⭐

Avinash Dixit. Thinking Strategically ⭐⭐⭐

星星标识的难易度仅供参考，反正作为一个穷鬼，我是买不起了。

1.1 积分游戏 Grade Game

本次课程的第一个博弈游戏来了~

Ben在课堂学生中下发了游戏材料，大体内容为：玩家需要和一个对手进行博弈，两人都需要在α和β之间选一个字母：

1）若两人均选α，则两人期末成绩均为B-；

2）若两人均选β，则两人期末成绩均为B+；

3）若一人选α，一人选β，则选α者得A，选β者得C。

由此，我们可以推出两个单人的博弈矩阵，合并后画出如下的完整博弈矩阵。

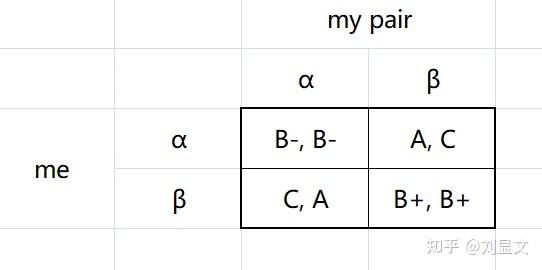
在这个矩阵中，每一个格子里左侧的代表“me”的收益，右侧的代表“my pair”的收益。

画出此矩阵后，出现了一个新的问题——玩家如何选择，应该取决于什么呢？换而言之，A、B+、B-、C这四种不同的成绩虽然有优劣之分，但如何进行量化呢？

举例来说，如果我选择了α，那么如果对手也选α，我的成绩为B-，如果对手选β，我的成绩为A，所以α选择下我的成绩为B-到A之间。如果我选β，同样的逻辑，我的成绩为C到B+之间。B-到A之间和C到B+之间，哪个更好呢？

所以，为了能够进行清晰的推演，我们必须把这些选择进行量化。

和经济学非常相似的一点在于，博弈论本身并没有对人们的价值导向（偏好）去进行规范的作用，它只是作为一种工具，在给定的偏好&收益下去进行逻辑推演。说人话就是，博弈论不在乎你是不是变态，博弈论只是帮助每一个变态在给定的各种条件下过得更好。

那么，我们按照功利主义的观念，将前文中的成绩进行量化，重新画出矩阵。此处假定大家都想要更高的成绩，并认为成绩A的收益为3，B+为1，B-为0，C为-1。

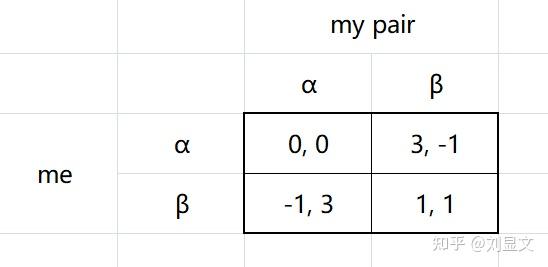
此时，我们再观察这个矩阵，就会发现，之前混沌的选择现在变成了一个简单的比大小游戏。

从我的角度出发看，假设已知对手选择α策略，我选α的收益为0（左上角0, 0中左边是我的收益），选β的策略为-1（左下角-1, 3中的-1是我的收益），0>-1，自然我应该选α；假设已知对手选β，此时我选α收益为3，我若选β收益为1，3>1，自然我还是应该选α。两个假设结合，也就意味着，无论对手选什么，我都应该选α。

另外一边来看，由于这个博弈矩阵中我的对手所面对的数字和我是一摸一样的，所以上述逻辑对我的对手来说也完全成立，这也就意味着我们一定会得出（α, α）这样的博弈结果。

此处，我们学到一个定义：

1.1* 严格优势策略 Strictly Dominant Strategy

Def: We say that my strategy α strictly dominates my strategy β if my payoff from α is strictly greater than that from β regardless of what others do.

如果α策略的收益在无论对手作何应对的情况下都高于β策略的收益，则α相对于β为严格优势策略。

从定义，我们可以推出第一个结论：

Lesson 1 : 不要使用严格劣势策略。

在这个博弈游戏中，我们除了假定大家有统一的、被量化了的偏好，还假定了大家都是理性人，会追求更高的数字。看到这里，想必很多人都能想起来囚徒困境，没错，这个模型和囚徒困境是一样的。

两者都出现了一个情况，在双方都选β就能得到(1, 1)的结果时，双方却都基于理性，选择了α，得到(0, 0)的结果，得到的更少了。

Lesson 2：理性的选择可能导致更糟的结果。

Ben举了个囚徒困境的美国校园例子，大学宿舍到了期末临近时卫生就会变得很糟（中国的大学宿舍应该不需要等到期末），因为大家都指望别人去打扫，这样自己可以占便宜。

同样，还有企业之间的价格战，也属于囚徒困境。

而针对囚徒困境的破解，常见的误区是沟通可以解决这个困境，然而在缺乏强制力介入的情况下，沟通缺乏意义，有效的三件套是有强制力的合同（条约）、重复博弈、教育（存疑）。

接下来，我们变化一个假设条件，来看看第一个博弈的变化。

如果假设说商学院里的同学们大多数是秉承功利主义思想，仅仅计较得失的“饭桶恶魔”（Evil Gits），那么，再假设一下，隔壁神学院里的同学都是秉承着某些含有利他主义精神的宗教原则，有高道德追求的“愤怒天使”（Indignant Angels）。

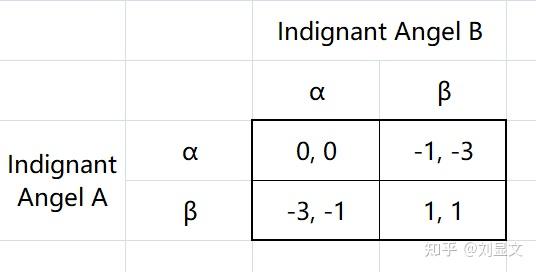
在这种情况下，若是天使A和天使B出现了(α, β)组合，既诚信+背叛组合。原本背叛者会获得3的收益，可是他内心的负罪感太重了，导致产生了-4的收益，最后收益变为3-4=-1。原本选择合作者会获得-1的收益，但是他对于背叛者的愤怒，恨不得开除对方教籍，产生了-2的情绪收益，最后收益变为-1-2=-3。

于是，两个愤怒天使之间就出现了协和谬误（Coordination Problem），α不再是严格优势策略。

这里，Ben推出了第三个结论，如果我们不知道一个人或一场博弈中的收益情况，那么我们就不可能获得收益。

Lesson 3：如欲得之，必先知之。

我看的时候感觉有两个小问题，第一个，两个愤怒天使互相背叛后的收益怎么会和两个恶魔互相背叛之后是一样的呢？第二个，Lesson 3为什么放在愤怒天使内战模型后面呢？放在成绩从字母ABC变为功利化的数字那一步逻辑不是更通顺么。

如果博弈是发生在饭桶恶魔和愤怒天使之间呢？

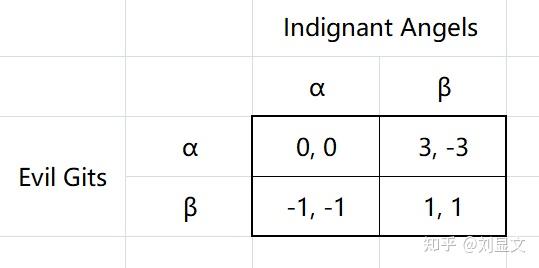
从矩阵中我们可以看到，对于饭桶恶魔来说，无论天使怎么选，α策略的收益依然是更高的，符合严格优势策略的要求。

可对于天使来说，恶魔选α时，天使也选α得0，选β得-3，恶魔选β时，天使选α得-1，选β得1，既不存在严格优势策略，那怎么办呢？无所谓。因为在这个博弈中双方都有完全信息，所以天使可以看到恶魔的博弈信息，能意识到恶魔一定会按严格优势策略选α，不需要考虑恶魔选β的情况，所以天使应该选α。

Lesson 4：进行换位思考。

在上述理性分析之下，Ben提到了一个现实中总结出来的数据，在亚利桑那大学进行的实验中，有70%的参与者选择了α，30%的参与者选择了β，而在耶鲁大学进行的实验中，238人选择α(87%)，36人选择β(13%)。

然后Ben嘲笑了一下亚利桑那大学的同学们，大概是在阳光下晒得太久了呆掉了。为了理解大佬的笑点，我还特意去查了一下背景资料......这大概是北大嘲笑中山大学荔枝吃多了变傻的那种感觉吧。

Lesson 5：耶鲁大学的学生比较邪恶。

这个Lesson 5我想了一下，应该是暗指，高智商或者精英群体更加懂得权衡利弊（自利）吧，有点符合前几年那个“精致的利己主义者”的味道。

定义：要形成一场博弈需要哪些要素呢？

1）参与者

2）策略：一般我们用 $s_{i}$ 来表达参与者i的某个特定策略， $S_{i}$ 则用来表达参与者i的全部策略集合，S则表达一次博弈（一局游戏），也可以叫策略组合。

3）收益： $U_{i}s$ 代表参与者i在s这一局博弈中的收益

4）假定的背景（已知）条件：每个人都知道其他人可能选择的策略，博弈者之间互相信息透明

5） $S_{-i}$ 用来表示一局博弈中除了参与者i之外其他所有人的策略

为了方便理解这些要素，我们来一起玩一局试试看。

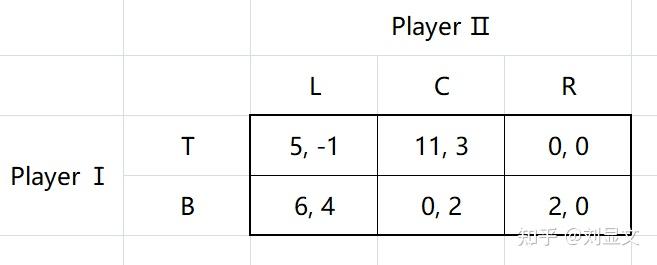
在这个矩阵中，我们可以整理出以下部分信息：

参与者：Player Ⅰ, Player Ⅱ

策略： $S_{Ⅰ}$ ={T, B} , $S_{Ⅱ}$ ={L, C, R}

收益： $U_{Ⅰ}$ (T, C)=11, $U_{Ⅱ}$ (T, C)=3

当我们有了这些定义和符号之后，我们就可以用另一种更严格的方式来表达之前所说的严格优势策略了。

Def: Player i's strategy $S'_{i}$ is strictly dominated by player i's strategy $S_{i}$ if :
$U_{i}$ ( $S_{i}$ , $S_{-i}$ ) > $U_{i}$ ( $S'_{i}$ , $S_{-i}$ ) for all $S_{-i}$

1.2 汉尼拔 Hannibal

现在，我们来看一个新的游戏，假定公元前三世纪时的迦太基将军汉尼拔有两个营的兵力，此时正从西班牙出发进军罗马，他有两条路可以选，一条是沿着相对宽阔的海岸线道路进军，另一条是翻越崎岖的阿尔卑斯山，如果选择了阿尔卑斯山的道路，那么路途中会由于地理、气候问题直接损失一个营的兵力。同样，罗马军队也可以选择且仅能在某一条路设防，假定他们猜对了，则可以让迦太基军队损失一个营的兵力。

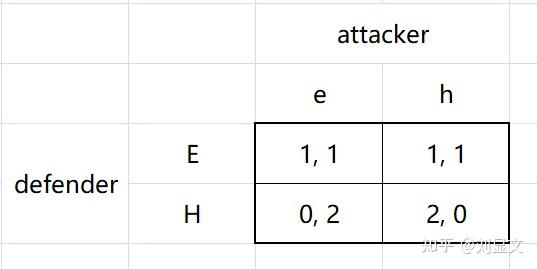
图中的e,E=easy , h,H=hard

我们先从罗马人的角度来看这个问题，按照矩阵中的信息，如果迦太基军队从海边的easy pass进军，那么罗马军队的最好选择是在海边设防，这样可以消灭迦太基一个营，收益为1，如果迦太基军队从阿尔卑斯山反过来，那么罗马军队最好的选择是在阿尔卑斯山设防，这样迦太基路上损失一个营，又被守军消灭一个营，罗马人收益为2。如此说来，罗马的选择应取决于迦太基怎么选，换而言之，此时罗马不存在严格优势策略。

再从迦太基人的角度看这个问题，假如罗马人在海边设防，则无论迦太基人走哪条路，都会损失一个营的兵力，收益为1，假如罗马人在山区设防，那么迦太基人走海边就可以零损失通过，收益为2。这么思考的话，迦太基人在事先无法探知罗马军队布防情况的条件下，应当选择走海边的宽阔大陆，这个选择的收益大于或等于走山区的收益。

所以反过来说，罗马人知道迦太基人一定会选海边进军，那么自然应该去海边布防。

换成术语表达，迦太基人选择海边进军的策略相较于山区进军的策略是——

1.2* 弱优势策略 Weak Dominate Strategy

Def Player i's strategy $S'_{i}$ is weakly dominated by her strategy $S_{i}$ if
$U_{i}$ ( $S_{i}$ , $S_{-i}$ ) $\geq$ $U_{i}$ ( $S'_{i}$ , $S_{-i}$ ) for all $S_{-i}$
$U_{i}$ ( $S_{i}$ , $S_{-i}$ ) > $U_{i}$ ( $S'_{i}$ , $S_{-i}$ ) for some $S_{-i}$

1.3 迭代剔除 Iterative Deletion

Ben要求全班的同学，每人选择一个1到100之间的数字，谁选的数字最接近平均数的三分之二，则获得胜利。

在这样一场多人博弈的游戏中，我们大体可以将思路分成几层。

第一层：

如果全班所有的同学是随机选择数字的，那么平均数应该落在50左右，50的2/3是33左右，所以选择33。

第一层思路核心问题在于，全班同学不会随机选择数字。

第二层：

如果我预计第一层的人很多，那么我应该顺着第一层的思路选择33的2/3，也就是22左右。

第二层预判了第一层的选择，但还是低估了其他玩家。

第三层：

首先剔除本局游戏中的弱劣势策略，也就是所有大于67的数字，因为哪怕所有人都选100，平均数的2/3也才近似于67，所以大于67的数字是不可能出现的。

第三层开始使用博弈论的框架了，并假设玩家是理性的，但是想得不够远。

第四层：

那么67以下选谁呢？67的2/3大概是45，可是，如果我们剔除了67以上的所有数字，那么同理，所有大于45的数字也不应该被选择，因为此时45-67之间所有的数字等价于第三层时67-100之间的数字，也变成了弱劣势策略。

按照这个逻辑继续往下思考，当45以上的数字被剔除后，45-30之间的数字又变成了新的弱劣势策略，然后递推到30-20、20-13......这个过程叫做迭代剔除劣势策略。

直到最后，所有人都会选择1。

第四层逻辑严谨，不仅假设玩家是理性的，并且所有人都认为其他玩家也是理性的。

PS：推到1这一步时，需要一个反复循环的思考过程——诸如我知道你知道我知道你知道我是理性的——术语叫共同知识（Common Knowledge）。

第五层：

但实际上这个发生在2007年的课堂实验平均数是13又1/3，所以平均数的2/3是9，远高于第四层的1。

同样的实验，在2003年的课堂上，平均值是18.5，2004年是21.5，2005年是23，这么看来07年的数字还是比较低的了。

也就是说，第四层的结果从来就没有达到过，为什么呢？

因为不是所有的参与者都是理性的，同样的事情在现实世界里比比皆是，如股票市场，一个人能精确的分析出企业的营收不一定能为自己带来股票买卖上的盈利，他必须要明白整个市场对此会作何反应才行。

所以在换位思考的实际应用中，我们不仅要理解其他参与者的利益&动机等要素，还需要理解其他参与者对于这场博弈有多老练，以及其他参与者认为我们有多老练等“共同知识”的问题。

共同知识 - Common Knowledge

举个实际应用例子，一家大型企业在与其他大型企业进行谈判类博弈时，通常会假设对手的水平很高，并作出相应的布置，如聘用专业的谈判专家，进行详尽的数据分析、严谨的背景调查等等。而在销售端口面对个体的客户时，通常会假设客户是非专业人士，并作出相应的布置，如培训一线销售人员练习针对所有客户的统一话术、掌握调动客户情绪的策略、逼迫客户现场买单的谈判技巧等等。

1.4 中位选民定理 The Median-Voter Theorem

假定现在有两个候选人要参加一场竞选，他们可以从1到10的十个数字从选择一个数字代表自己的立场，越小的数字代表观点越偏左翼，越大的数字代表观点越偏右翼，每个数字背后假定都有10%的选民支持该数字所在的立场。选民投票的思路很简单，投给和自己所在立场最接近的候选人，若两个候选人平局，则一人获得一半选票。两个候选人的目标是最大化自己得到的票。

在这个模型中，依据前面的内容，我们会发现，两个极端位置，1和10是劣势策略。

我们推导来看看，A选择2的策略是否优于选择1的策略。

当候选人B选择1时： $U_{A}$ (1, 1) = 50% < $U_{A}$ (2, 1) = 90% ✔

当候选人B选择2时： $U_{A}$ (1, 2) = 10% < $U_{A}$ (2, 2) = 50% ✔

当候选人B选择3时： $U_{A}$ (1, 3) = 15% < $U_{A}$ (2, 3) = 20% ✔

当候选人B选择4时： $U_{A}$ (1, 4) = 20% < $U_{A}$ (2, 4) = 25% ✔

以B选择1的情况为例翻译一下，A和B都选1的话，A的收益U为50%的得票，当A选2而B选1时，A获得的收益U为90%的得票，结论，B选1时，A选2的得票高于A选1的得票。

后续5、6、7、8、9、10以此类推。

这里还有一个有趣的现象，当B没有选1或2时，A选2的得票永远比1多5%。

结论：选2的策略严格优于选1的策略。

同理，9和10与2和1是对称的，所以选9的策略也会严格优于选10的策略。

那么，选3会优于选2么？

以同样的推导过程来看看。

当候选人B选择1时： $U_{A}$ (2, 1) = 90% > $U_{A}$ (3, 1) = 85% ×

好了，不用往下看了，不成立。

但是，若是考虑迭代剔除的问题，既，由于1和10这两个策略是劣势策略，不会有人选，那么接下来会如何？

当候选人B选择2时： $U_{A}$ (2, 2) = 50% < $U_{A}$ (3, 2) = 80% ✔

当候选人B选择3时： $U_{A}$ (2, 3) = 20% < $U_{A}$ (3, 3) = 50% ✔

当候选人B选择4时： $U_{A}$ (2, 4) = 25% < $U_{A}$ (3, 4) = 30% ✔

当候选人B选择5时： $U_{A}$ (2, 5) = 30% < $U_{A}$ (3, 5) = 35% ✔

后续6、7、8、9、10以此类推。

这时，我们会发现，尽管2和9的策略不是全局的劣势策略，但如果我们意识到1和10由于本身是劣势策略而不会有人选的事实，则2和9也会成为实际上的劣势策略。

同样的逻辑，我们很容易意识到，3和8、4和7都会成为劣势策略，最终只能选择5或6，由此我们得出中间选民定理。

在经济学领域，有一个与之非常类似的产品布局模型。如加油站的位置选取问题，直觉来说，加油站应均匀分布以获取更多的客流量，可是由于不同加油站之间的竞争，我们会发现现实中的加油站常常聚在一起，这是为了避免自己由于位置相对不好而被淘汰，就是中间选民定律所揭示的情况。

关于中间选民定律Ben老师的课外阅读推荐：

Anthony Downs. Political Science. 1957

Hotelling. "Economics". 1929

但中间选民定律所依赖的模型本身有不少问题。

1）选民不太可能是均匀分布的；

2）候选人并不总是只有两个；

3）会有不投票的选民；

4）候选人无法随意更改自己的立场，选民们会依据他过往的历史而非口号进行判断；

eg: 1997年前，英国工党在竞选中频频失利，时任工党党魁布莱尔为了说服大众工党现在是一个走中间路线的党派，应竞选规则中党派必须公布自己未来五年的财政计划之要求，直接照抄了当时执政党保守党的财政计划进行公布......

5）选民投票的依据是多维的，并不只关注左右；

6）会有初选。

1.5 最优反应 Best Response

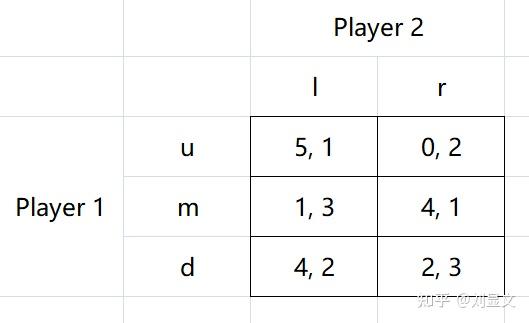
在这个模型中，通过观察我们发现两名玩家都没有优势策略，这时我们要如何决断呢？

从玩家1的视角出发，如果玩家2选了l策略，那么1选u获得5收益为最大，如果玩家2选了r策略，那么2选m获得4收益为最大。可是，在不知道2的策略前提下，1选d的策略看起来最稳妥。

如果假定玩家2选择l和r的概率对半开：

玩家1选择u策略的期望收益 = 50%*5+50%*0 = 2.5

玩家1选择m策略的期望收益 = 50%*1+50%*4 = 2.5

玩家1选择d策略的期望收益 = 50%*4+50%*2 = 3

此时易知d为玩家1的最佳选择。

如果玩家2选l和r的概率不是对半开呢？没关系，我们可以通过一张图表来表达所有情况。

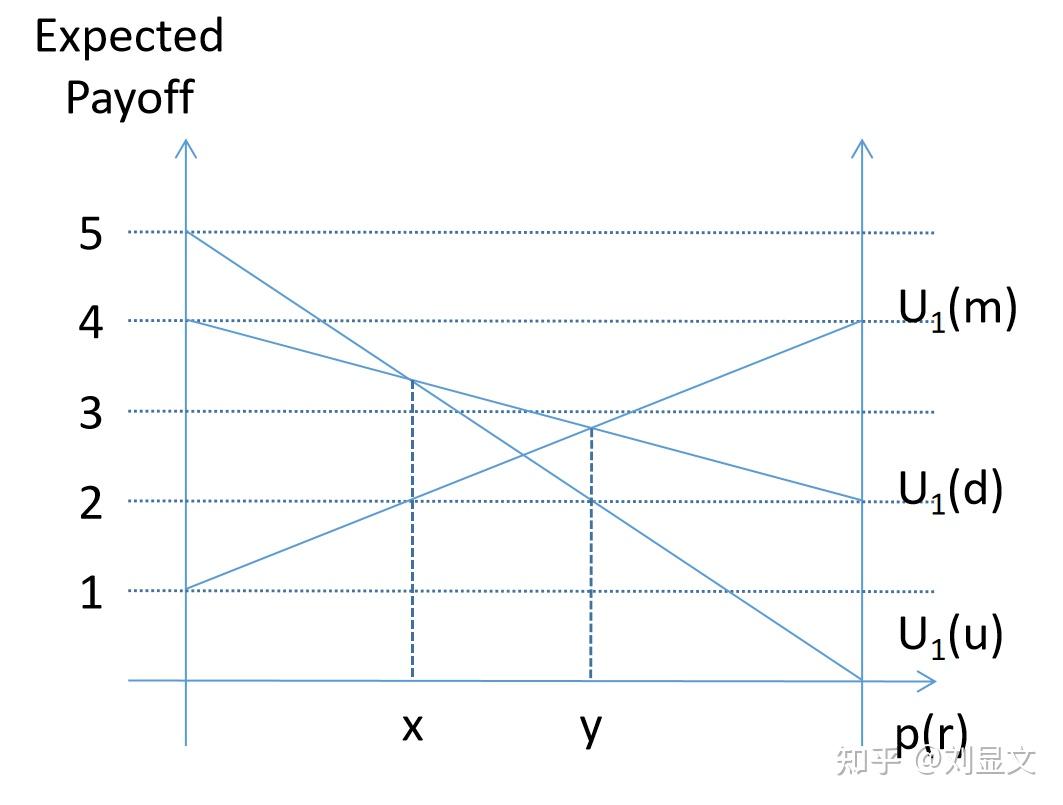
图中的X轴表示玩家1认为的，玩家2选择r的概率（p(r)），左侧交汇点为0%，右侧交汇点为100%。

Y轴表示玩家1的期望收益。

按照左侧起点从上到下的顺序，三条直线的表达式分别为：

$EU_{1}$ ( u, p(r)) = (1-p(r))*5+p(r)*0

$EU_{1}$ ( d, p(r)) = (1-p(r))*4+p(r)*2

$EU_{1}$ ( m, p(r)) = (1-p(r))*1+p(r)*4

此时，我们可以直观的看到，出现了两个重要的交叉点，x和y。

按照两式联立的方法可以得出x=1/3，y=3/5。

得出结论

当p(r)<1/3时，玩家1选择u策略收益最大

当1/3<p(r)<3/5时，玩家1选择d策略收益最大

当3/5<p(r)时，玩家1选择m策略收益最大

2. 纳什均衡 Nash Equilibrium

2.1 点球大战 Penalty Kick Game

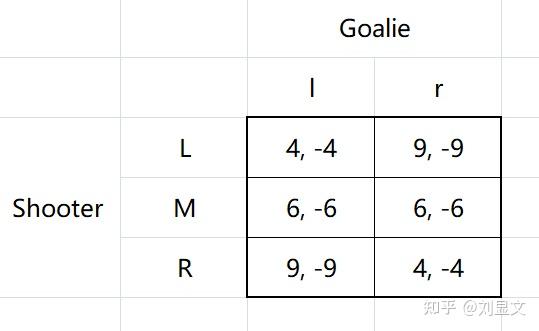
假定这个矩阵代表一场足球比赛中的点球大战情况，数字代表进球的可能性，如4可看作40%概率进球，反过来对于守门员，-4代表40%概率失分。

首先我们会发现，这里双方都不存在优势策略，于是我们试着用最优反应的角度来分析。

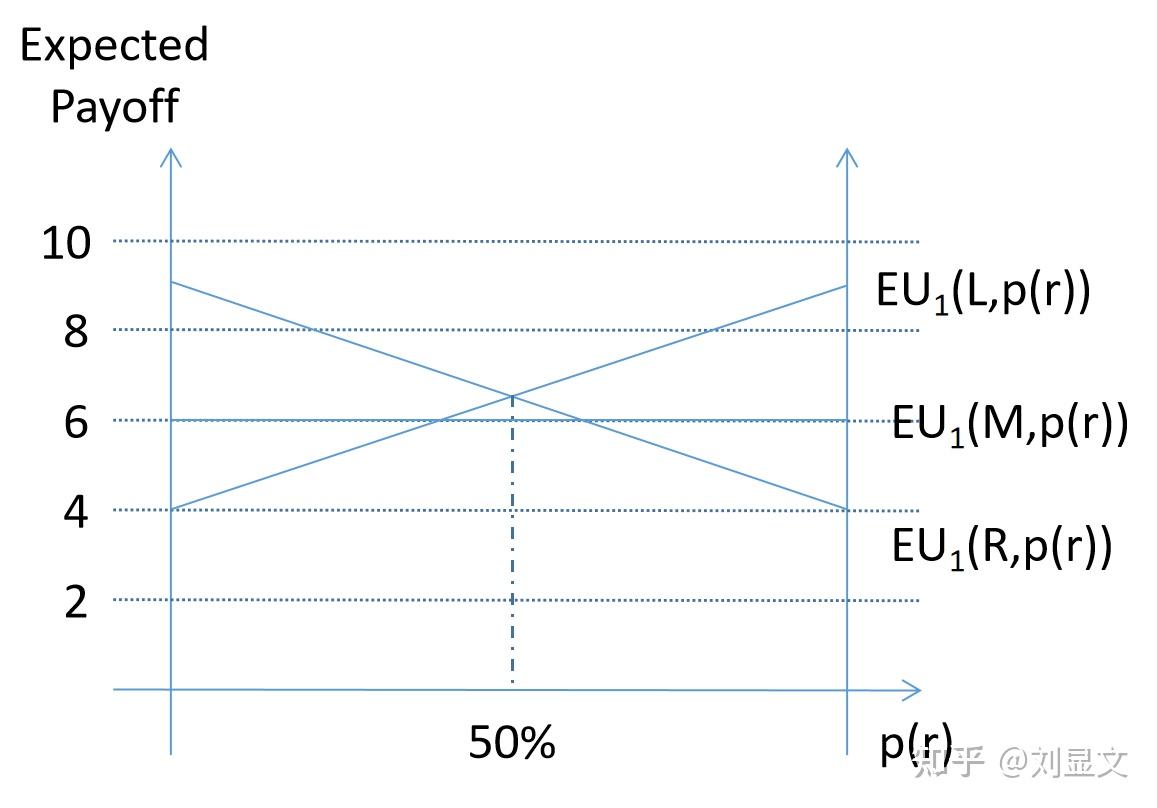
X轴代表进攻方认为的，守门员向右侧(r)扑救的概率，从左到右为0%到100%。

Y轴代表的是进攻方得分的概率，从下到上为0到10，也可以说是0%到100%。

再根据矩阵中的数字，画出三条分别代表进攻方使用左(L)、中(M)、右(R)三种不同策略的直线。

从这里我们可以观察到，进攻方选择M，也就是对着正中间射门在任何情况下都不是最优反应。

至于选择L还是R，则取决于进攻方的预判，若射门球员认为守门员扑救左边(l)的概率大于50%，那就射右边，反之则射左边。

Lesson 1：不要选择一个在任何情况下都不是最优反应的策略。

当然，和现实世界对比，这个模型忽略了很多实际问题，如惯用脚、球速对于进球率的影响等。

接着我们看一个真实数据，根据Chiappori发表在美国经济评论(AER)的一篇论文，有如下表格：

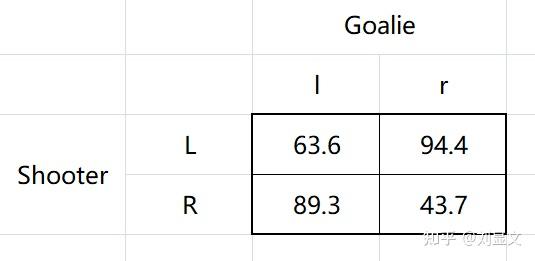
这里的L代表射门球员的“自然方向”，既右撇子的L统计的是他的左侧，左撇子的L统计的是他的右侧。

图中的数字代表统计出来的进球率。

Ben还提到这里的数据一半来自意大利的"强队"，一半来自法国的"弱队"（日常乳法✔）。

由此我们可以引出最优反应的定义。

Def Player i's strategy $S''_{i}$ is a BR to the strategy $S_{-i}$ of other players if
$U_{i}$ ( $S''_{i}$ , $S_{-i}$ ) $\geq$ $U_{i}$ ( $S'_{i}$ , $S_{-i}$ ) for all $S'_{i}$ is $S_{i}$
or $S''_{i}$ solves max $U_{i}$ ( $S_{i}$ , $S_{-i}$ )

而一个更广义上的定义可以写作：

Def Player i's strategy $S''_{i}$ is a BR to the belief P about the others' choices if
$EU_{i}$ ( $S''_{i}$ , P) $\geq$ $EU_{i}$ ( $S'_{i}$ , P) for all $S'_{i}$ is $S_{i}$
or $S''_{i}$ solves max $EU_{i}$ ( $S_{i}$ , P)

举例： $EU_{1}$ ( $L_{1}$ , p) = p(l) $U_{1}$ (L, l) + p(r) $U_{1}$ (L, r)

实话实说，虽然前后内容都能理解，但一进入公式环节，我感觉自己快瞎了。

2.2 合伙人游戏 Partnership Game

设两人共同持有一家公司的股份，平分利润。

两人各自都要决定为这家公司投入多少精力，用数字0到4来表示投入程度， $S_{i}$ [0,4]，这里的0到4是连续性的，既可以出现1.21123或3.42245这样的程度，而非前面案例中只有整数可选。

这家公司的利润为：

Profit = 4*( $S_{1}$ + $S_{2}$ +b* $S_{1}$ $S_{2}$ )

此处b代表1+1>2的·协同效应，设 0 $\leq$ b $\leq$ 1/4

两人的收益分别为：

$U_{1}$ ( $S_{1}$ , $S_{2}$ ) = 1/2*[4*( $S_{1}$ + $S_{2}$ +b* $S_{1}$ $S_{2}$ )] - $S_{1}^{2}$

$U_{2}$ ( $S_{1}$ , $S_{2}$ ) = 1/2*[4*( $S_{1}$ + $S_{2}$ +b* $S_{1}$ $S_{2}$ )] - $S_{2}^{2}$

现在，我们从1号玩家也就是 $S_{1}$ 的角度出发，我们要如何在2号玩家策略既定的情况下实现自身利益最大化呢？

将 $S_{2}$ 视为常数，对 $U_{1}$ ( $S_{1}$ , $S_{2}$ ) 的公式求导，令其等于0，函数为极值时，一阶导数为0。

对1/2*[4*( $S_{1}$ + $S_{2}$ +b* $S_{1}$ $S_{2}$ )] - $S_{1}^{2}$ 求导：

$\Rightarrow$ 2(1+b $S_{2}$ ) - 2 $S_{1}$

对2(1+b $S_{2}$ ) - 2 $S_{1}$ 求导：

$\Rightarrow$ -2 < 0

二阶导数为负，所以一阶导数为0时可求出极大值。

2(1+b $S_{2}$ ) - 2 $S_{1max}$ = 0

$S_{1max}$ = 1+b $S_{2}$ = $BR_{1}$ ( $S_{2}$ )

同理可得 $S_{2max}$ = 1+b $S_{1}$ = $BR_{2}$ ( $S_{1}$ )

在一开始的时候，我们给出了b的区间，现在取b=1/4的情况，以 $S_{1}$ 为X轴，以 $S_{2}$ 为Y轴来画图，看看会得出什么。

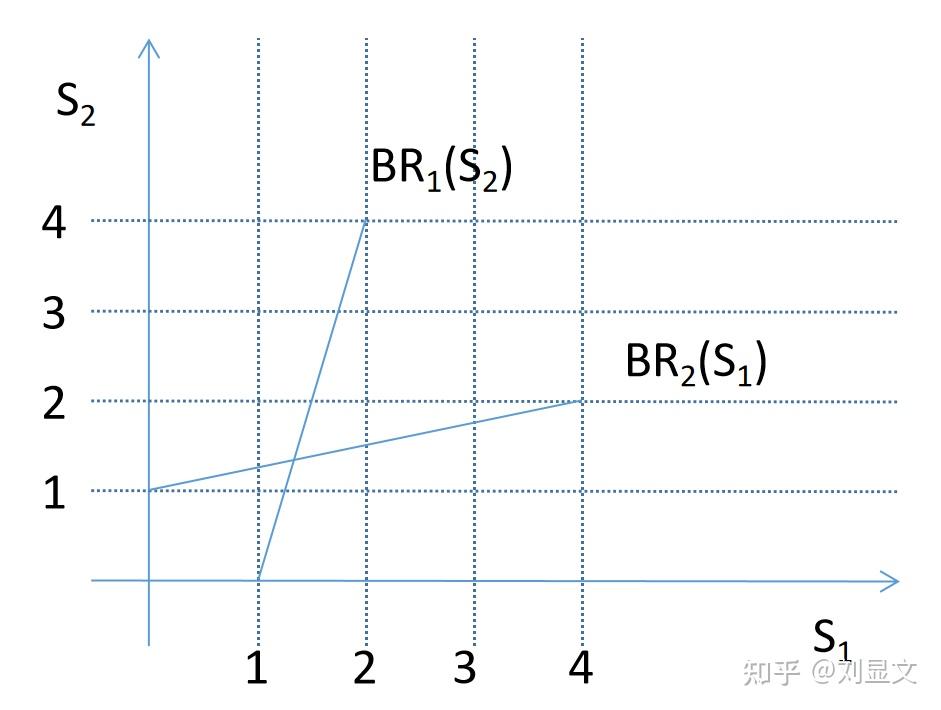
从最优反应的角度出发看 $S_{1}$ 的选择，当 $S_{2}$ 取[0,4]之间的最小值，等于0时， $BR_{1}$ (0) = 1，所以所有小于1的投入都不是最优反应。

同样，当 $S_{2}$ 取[0,4]之间的最大值4时， $BR_{1}$ ( 4 ) = 2，这也就是说，所有大于2的投入也都不是 $S_{1}$ 的最优反应。

同理， $S_{2}$ 的最优反应也不会小于1或大于2。

那，我们把所有非最优反应的部分统统剔除出去，只留1< $S_{1}$ <2和1< $S_{2}$ <2的部分，看看图会变成什么样的。

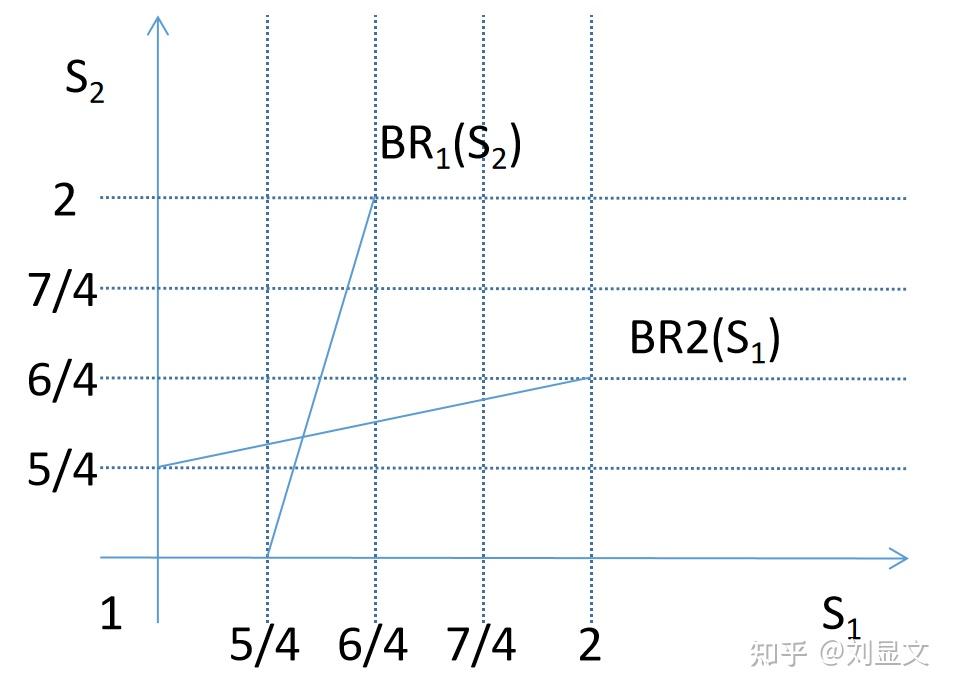
我们发现，这张图和上一张除了数字不同，其他的一模一样，也就是说，以排除非最优反应的逻辑来推导的话，我们又可以把小于5/4和大于6/4的部分继续剔除，然后接着往下套娃。

那还是不套了。

无限套娃最后的结果是无限接近两条直线的交点，那么我们直接求交点的解。

$S_{1max}$ = 1+b $S_{2max}$

$S_{2max}$ = 1+b $S_{2max}$

$S_{1max}$ = $S_{2max}$

$\Rightarrow$ $S_{1max}$ = $S_{2max}$ =1/(1-b) $\approx$ 1.33

现在，我们再看看交汇点，这里所代表的即是纳什均衡(Nash equilibrium)。

这是指，博弈双方达成了平衡，都不想偏离这个点的一种情况。博弈双方都达到了最优反应点。

这一段的数学推理很让人感到舒畅，唯一困惑我的点在于，预设条件中的收益公式“ $U_{1}$ ( $S_{1}$ , $S_{2}$ ) = 1/2*[4*( $S_{1}$ + $S_{2}$ +b* $S_{1}$ $S_{2}$ )] - $S_{1}^{2}$ ”是怎么来的呢？

在上述给定的条件下，我们发现，一对合伙人在[0,4]这个投入区间里，都应该选择1.33水平的投入，才能达到自己的利益最大化。很明显，单纯从公司整体收益的角度来看，这不是一个好事情。

为什么会有这个结果呢？

这既不是因为工作量的多少，也不是协同效应的问题，而是由于努力工作的人只能获得50%的边际产出，换而言之，这是因为在给定合伙人努力程度的前提下，我任何多一份的努力都需要自己承担100%的边际成本，而只能享受到50%的边际产出。

这种现象在经济学中被称之为外部性(Externality)。

如果b代表的协同效应变化了会怎么样呢？假定它下降了。

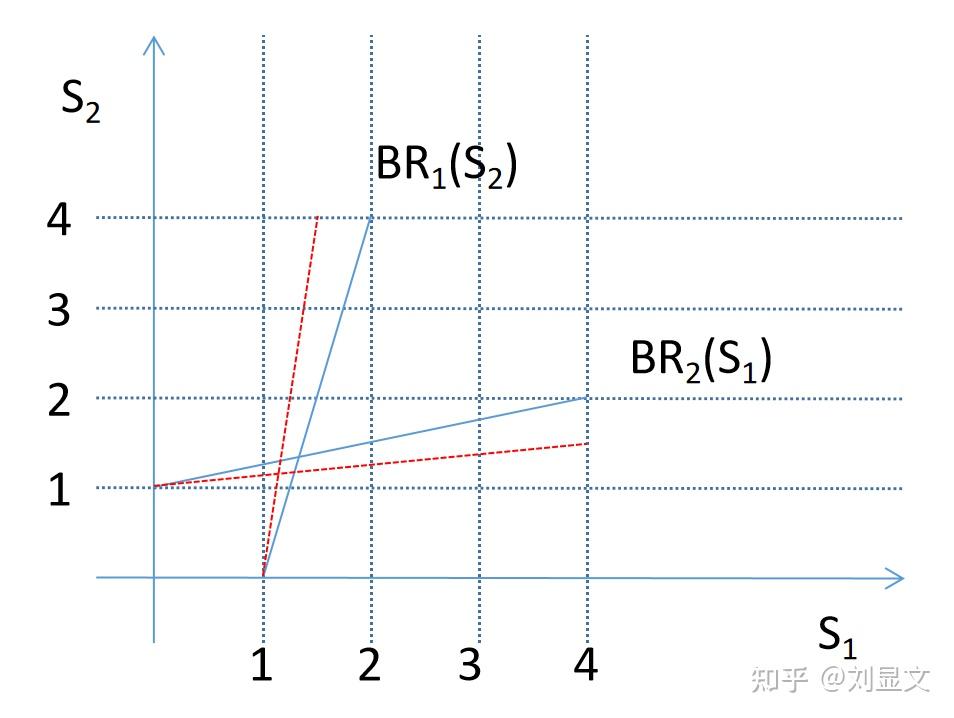
这里我们可以看到，如果b值变小，那么 $S_{1}$ 的曲线会往垂直方向运动，而 $S_{2}$ 会向水平方向运动，导致两者的交汇点更接近原点，也就是说两个合伙人投入的努力会变少。

依据前文，我们对纳什均衡(Nash equilibrium)给出如下定义：

Def A strategy profile ( $S_{1}^{*}$ , $S_{2}^{*}$ .... $S_{n}^{*}$ ) is a NE
if for each i, her choice $S_{j}^{*}$ is a best response to the other players' choices $S_{-j}^{*}$

掌握纳什均衡对我们有什么价值呢？

1）在一场博弈中选择了纳什均衡策略的玩家无需后悔，因为无论如何他的状况不会更好了；

2）纳什均衡是一个自我实现的信念，既博弈双方都认为事情会如此发展，最后事情也确实如此发展了；

3）现实中博弈的结果会不断的趋近纳什均衡。

我们通过一个例子来进一步认识一下NE：

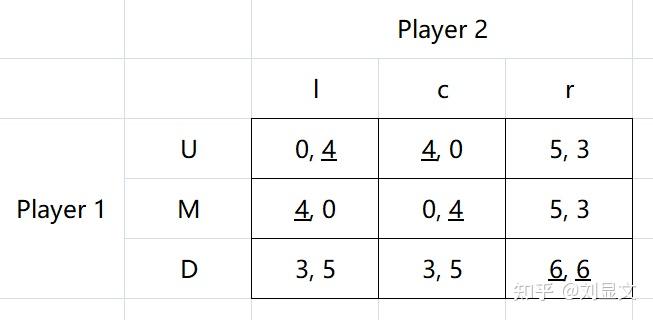
要找到一场博弈中的NE，首先我们要找到BR。

图中所有带下划线的数字既代表着BR选择，如假定Player2选择l时，Player的BR为M，此时收益为4，写作：

$BR_{1}$ (l) = M = 4

同理，写出所有的BR：

$BR_{1}$ (l) = M = 4 $BR_{2}$ (U) = l = 4

$BR_{1}$ (c) = U = 4 $BR_{2}$ (M) = c = 4

$BR_{1}$ (r) = D = 6 $BR_{2}$ (D) = r = 6

无论是通过图，还是公式，我们都会发现，两个博弈者有一个BR重叠之处，就是D&r的组合，这便是这一局博弈的NE，写作NE=(D,r)。这里因为是非连续性的变化，所以找到点即可，前面例子中因为是连续性变化，所以找到两条线的交点即可。

同时，由于这个案例中，玩家1和玩家2的每一个策略都是某些时候的最佳策略，所以排除劣势策略和排除非最优回应的方法都有些行不通。

Ben还提到，不能想当然的认为，哪怕是理性的人，就能自然而然的达成纳什均衡，还需要更多条件才行，不过此处他没有展开讲解了。

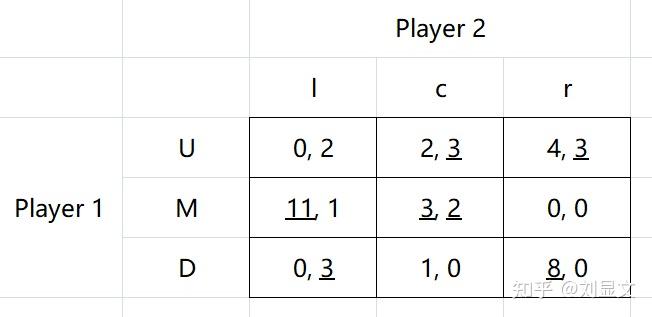
再看一个例子，以上一例中同样的逻辑，我们用下划线把所有的BR标出来，很快找到NE=(M,c)。

接下来，我们试试把纳什均衡和优劣势策略放到一起来看。

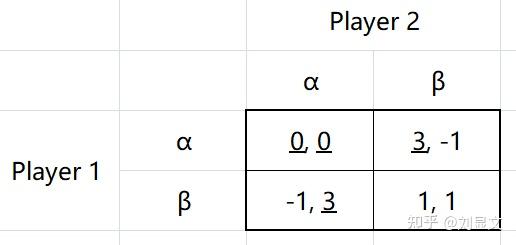
我们使用囚徒困境的矩阵进行展示：

这个矩阵中，我们已经证明了β相较于α是严格劣势策略。

同时，我们也可以用BR找出NE，得出NE=(α,α)。

根据定义，严格劣势策略不可能是BR，自然，也就不可能实现NE。

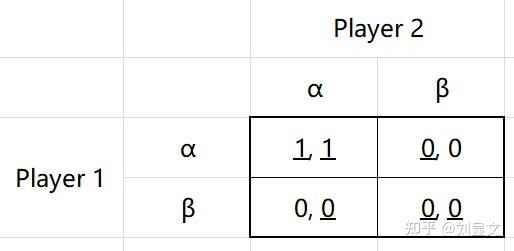
我们改变一下数字，来看看一个新矩阵。

还是先看所有用下划线标出来的BR，我们很容易判断(α,α)是NE，然而，根据NE的定义，我们发现这个矩阵中，(β,β)也是NE，因为当博弈双方处在这个位置时，任何一方单独改变策略都无法改善自身情况。所以，尽管NE是从BR这个概念推出来的，可它可以不符合自然语言中的最优情况。

2.3 投资游戏 Investment game

博弈者：全班同学

策略：投资0元或投资10元

收益：如果投资0元，收益为0元

如果投资10元，且全班有90%或以上的同学选择了投资，每人获得5元净利润

如果投资10元，且全班没有90%或以上的同学选择了投资，每人获得-10元净利润

面对这个游戏，稍加思考，我们会意识到NE有两种情况：要么所有人都投资，要么所有人都不投资。这就很好的解释了上一个矩阵例子中为什么(1,1)和(0,0)都是NE的问题。

所有人都不投资的NE相较于所有人都投资的NE处于帕累托劣势(Pareto dominated)。

在这个游戏里，初始情况变得非常重要，若是一开始时，只有一半的人选择投资，那么所有人都不投资的NE就会很快实现，但若一开始，有95%的人选择投资，那么所有人都投资的NE就会实现，这就很类似股市或者宏观经济中的预期问题了。我预测他人都不看好这家公司的股票，所以我也不看好它，所以自我实施的预测阻止我买入或鼓励我卖出这家公司的股票，最后股价下跌成为现实。

和囚徒困境的模型相比，投资者游戏中有两个NE，而囚徒困境中背叛永远是最优解，这种类型的博弈叫做协调博弈(Coordination game)。

在现实世界中，如腾讯的QQ和微信，在面世后就会面对协调博弈，安装的这些沟通软件的人必须要大于一个阈值，彼此才会有收益。再比如股票交易所，如果上市的公司数量、交易量等大于阈值，则会形成良性循环，如果没有......请参考北交所。再比如银行挤兑的问题，储户要么都不跑，要么一起跑，很多历史案例中银行本身并没有问题，但是由于预期变化，储户们选择了一起跑的那个NE，然后银行就凉凉了。

还是和囚徒困境相比，协调博弈中，沟通是可以改善大家的选择的（领导力在此处可以起到关键作用），因为协调博弈中大家是从一个NE更换到另一个NE，而非囚徒困境中的从优势策略更替为劣势策略，并且由于符合自身利益的特点，NE不需要外界强制力，人们会依据自身的利益对其进行选择。

合伙人游戏和投资者游戏都有一个特点，既对方投入的越多，那么“我”也愿意投入的越多，都就于策略互补类博弈(Strategic complements)。

2.4 性别大战 Battle Of Sex

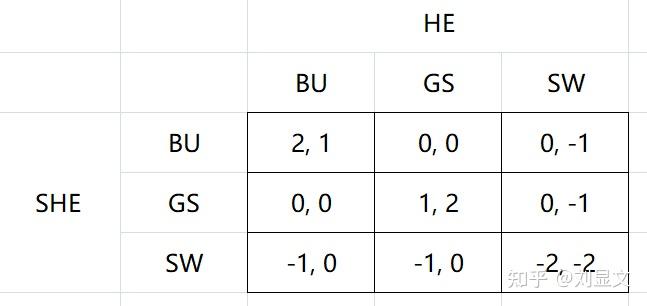
一对小情侣约会去看电影，现在有三部电影供他们选，武戏居多的谍影重重Bourne Ultimatum，文戏居多的特工风云Good Shepherd，以及动画片白雪公主Snow White。女孩儿偏好看BU，男孩儿偏好看GS，至于SW.....不太适合约会场合，若两人相约去看这部片，则彼此都会很尬。

但是，这对小情侣犯了一个错误，没有在事先约好一起去看哪部电影，于是现在他们两人要依据矩阵收益，去选择自己应该去哪个播放厅（假定你进去了就不能换播放厅）找对方。

参考已知信息，我们首先可以做出判断，SW是属于严格劣势策略，显然不应选，所以就只需要在BU和GS之间进行选择。

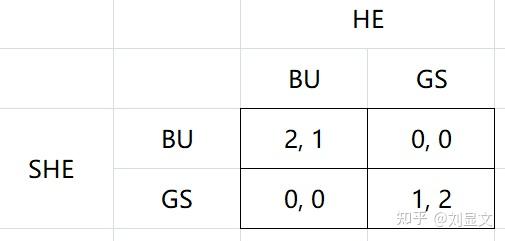
此时，我们发现有两个纳什均衡的情况，双方都选择看谍影重重或者双方都选择看特工风云，可与之前讨论的例子相比，出现了一个新情况，博弈双方在两个NE之间有利益冲突。

例如现实中劳资双方产生了利益冲突导致罢工，很多情况下，结束罢工其实对大家都有好处，可是怎么结束，以什么条件结束罢工，就属于双方利益冲突的点了。

2.5 古诺双寡头模型 Cournot Duopoly

在经济学中，古诺双寡头模型是一种用于研究介乎于完全竞争市场和垄断市场之间情况的模型，在19世纪时多数的产品领域都符合这种情况。

博弈者：两家公司

策略：选择某种同质化产品的产量 $q_{1}$ 及 $q_{2}$

生产成本：假定边际成本为常数c，所以生产成本等于c*q

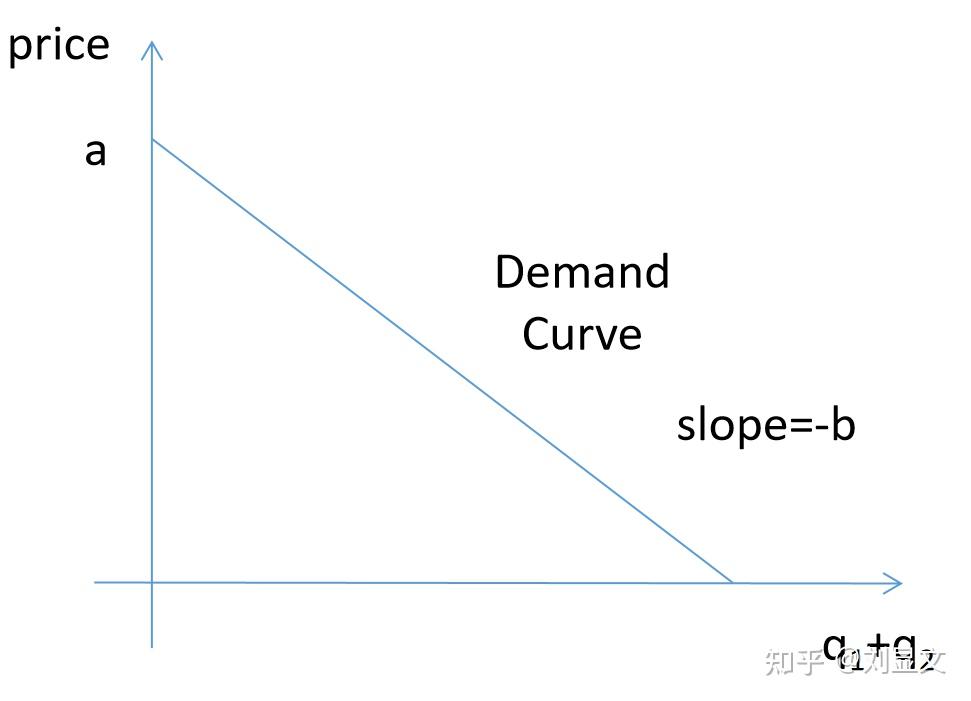
市场价格：p = a - b * ( $q_{1}$ + $q_{2}$ )

其中a&b均为常数，所以我们可以以 $q_{1}$ + $q_{2}$ 所代表的市场总产量作为X轴，价格作为Y轴作图，得：

收益：两家公司都希望最大化自己的收益，而收益=价格-成本，所以

$U_{1}$ ( $q_{1}$ , $q_{2}$ ) = [p]* $q_{1}$ - c* $q_{1}$

将价格公式代入，得

$U_{1}$ ( $q_{1}$ , $q_{2}$ ) = a* $q_{1}$ - b* $q_{1}^{2}$ - b* $q_{1}$ $q_{2}$ - c* $q_{1}$

为了求出最大化的收益，我们首先针对 $q_{1}$ 求导，并设结果为0

a - 2b* $q_{1max}$ - b* $q_{2}$ - c = 0

为了验证这是极大还是极小，再进行二阶求导

$\Rightarrow$ -2b < 0

由于b和a都是大于0的常数，二阶求导结果小于0，结果确为极大值

$\Rightarrow$ $q_{1max}$ = ( a - c )/2b - $q_{2}$ /2 = $BR_{1}$ ( $q_{2}$ )

同理可得 $q_{2max}$ = ( a - c )/2b - $q_{1}$ /2 = $BR_{2}$ ( $q_{1}$ )

在继续之前，我们先看一眼上一张图，加工一下。

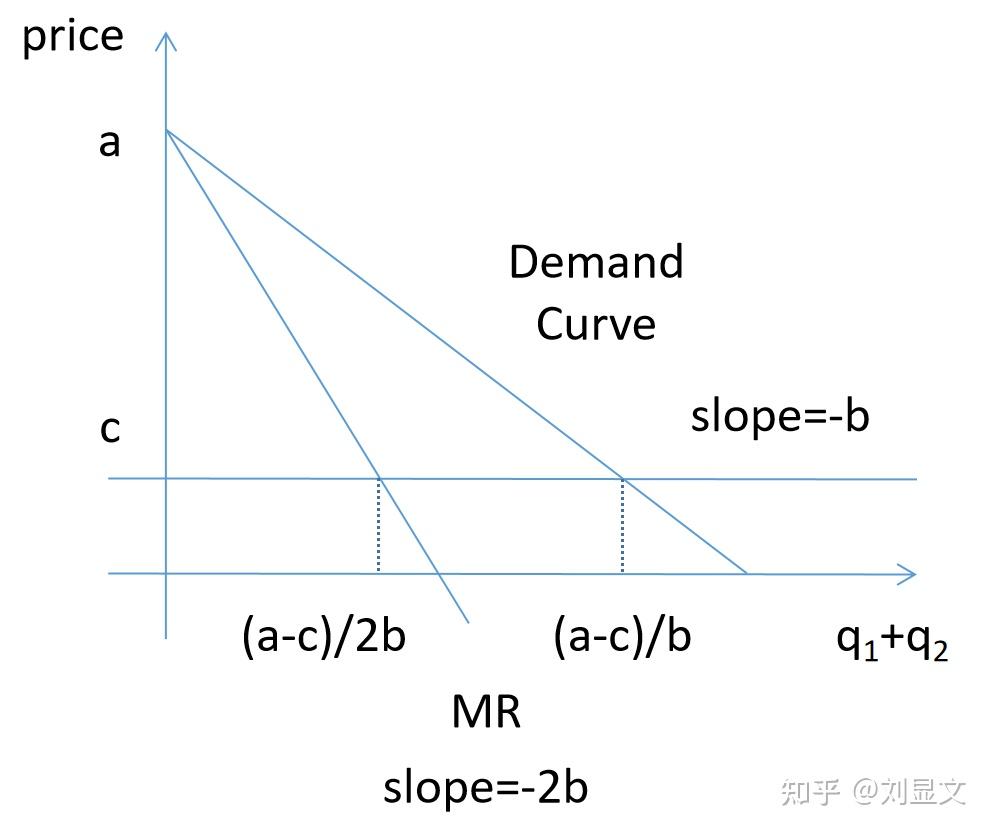
加入了c这一条代表边际成本的直线后，我们首先可以看到在在p=c的时候，根据需求线可求出此时的产量

b=Y/X $\Rightarrow$ b=(a-c)/Q $\Rightarrow$ Q=(a-c)/b

又知 AR=p=a-b*q

R=p*q=a*q-b* $q^{2}$ $\Rightarrow$ MR=a-2b*q

所以，可以推出MR与c相交时，产量为( a - c )/2b，这代表着垄断产量。

而AR与c相交时，产量为 ( a - c )/b，这代表着完全竞争下的产量。

注：MR=MC时，代表利润最大化，AR=MC时，代表收支持平。

再看我们计算收益时的结果，若是一家公司决定不生产，退出市场，则另一家公司的产量变为：

$BR_{1}$ ( $q_{2}$ =0 ) = ( a - c )/2b - 0/2 = ( a - c )/2b

此时，市场变为垄断。

那么，如果一家公司决定扩大生产，逼迫对方主动退出，它需要达到什么产量呢？

$BR_{1}$ ( $q_{2}$ ) = ( a - c )/2b - $q_{2}$ /2 = 0 $\Rightarrow$ $q_{2}$ = ( a - c )/b

此时，市场总产量等同于完全竞争市场产量。

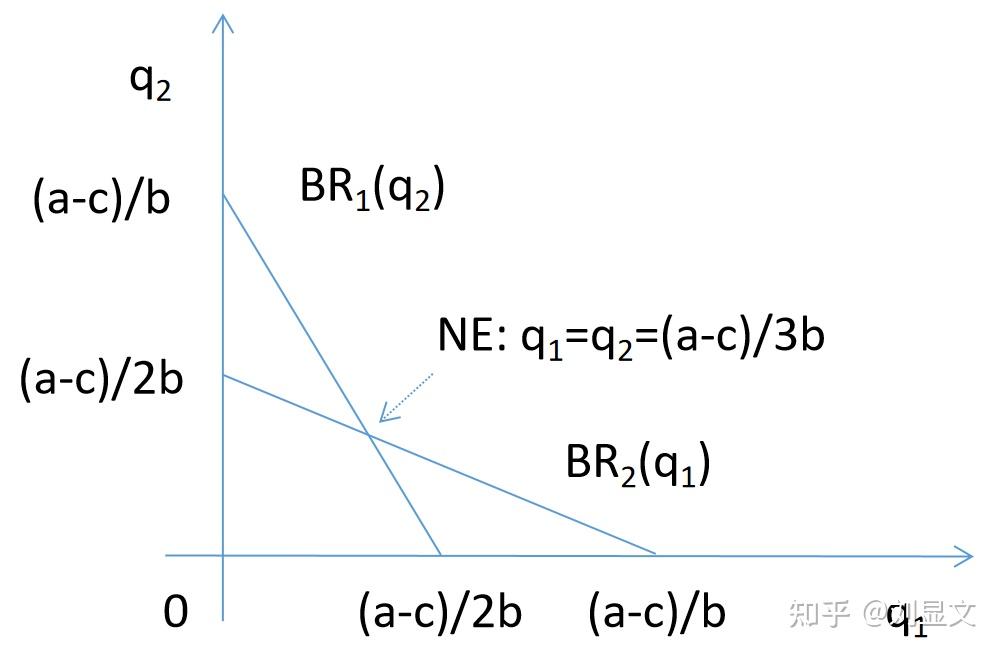
依据已知信息，我们以 $q_{2}$ 为Y轴， $q_{1}$ 为X轴作图，画出双方BR的反应。

此时，依照定义，NE应为双方BR交汇处，也就是图中的交点。此时：

( a - c )/2b - $q_{2}$ /2 = $BR_{1}$ ( $q_{2}$ ) = $BR_{2}$ ( $q_{1}$ ) = ( a - c )/2b - $q_{1}$ /2

( a - c )/2b - q/2 =q

$\Rightarrow$ q=(a-c)/3b

这既是古诺产出(Cournot Quantity)

合伙人游戏和投资者游戏中，博弈双方产出会互相正向影响，所以我们称之为策略互补类博弈(Strategic complements)，但在古诺模型中，博弈双方的产出互相负向影响，这种博弈被称之为策略替代类博弈（Strategic Substitutes）。

这里不是指双方生产的产品互为替代品（虽然这个例子里的确如此），而是指双方所使用的策略互为替代——你策略中产量越高，我的就越少，反之亦然。

现在，市场上两家寡头的产量都是(a-c)/3b，所以，市场总产量是2(a-c)/3b。

( a - c )/2b < 2(a-c)/3b < ( a - c )/b

古诺产出大于垄断产出，小于完全竞争市场的产出。

而垄断产出时，MR=MC，利润是最高的，这会不会导致两家寡头联手控制产量，减少总产出呢？

假定两家寡头约好，每家只生产( a - c )/2b的产量，实现行业整体利润最大化。那么很快，双方就都会有背叛对方的动机，因为( a - c )/2b不是任何一家的最优反应，此时“我”单方面提高产量，就能得到更高的利润。这意味着在没有其他因素介入的情况下，这种双寡头之间的合作是不可能的。即便双方通过合同，达成了垄断产量，依照十九世纪末期美国的历史经验来看，很快，这个行业就会由于存在经济利润(Economic profit)导致被新的挑战者入侵，使得产量扩大，合作失败。

2.6 伯川德模型 Bertrand competition

伯川德模型与古诺模型相同之处在于，都是描述不完全竞争市场的，差异之处则是，古诺模型下厂家决定产量，而市场价格是随着市场总产量的变化而变化的，伯川德模型中，厂家决定的是自己的价格，然后再看这个价格下能卖出去多少。

博弈者：两家公司

策略：选择某种同质化产品的价格 $p_{1}$ 及 $p_{2}$ ，并假定 0 $\leq$ $p_{i}$ $\leq$ 1

生产成本：假定边际成本为常数c

市场总需求量： $Q_{p}$ = 1 - $p_{lower}$ , $p_{lower}$ 代表两家公司中价格较低的那个

单个公司销售量： $q_{1}$ = 1 - $p_{1}$ , if $p_{1}$ < $p_{2}$

= 0 , if $p_{1}$ > $p_{2}$

= ( 1 - $p_{1}$ ) / 2 , if $p_{1}$ = $p_{2}$

两家公司互为镜像，所以 $q_{2}$ 同理。

收益：收入-成本= [ $q_{1}$ ]* $p_{1}$ - [ $q_{1}$ ]*c = [ $q_{1}$ ]*( p - c )

我们分情况来看一下此时的BR

$BR_{1}$ ( $p_{2}$ ) = $p_{1}$ > $p_{2}$ , if c > $p_{2}$

$p_{1}$ = $p_{2}$ - ε , if $p_{monopoly}$ $\geq$ $p_{2}$ > c

$p_{monopoly}$ , if $p_{2}$ > $p_{monopoly}$

$p_{1}$ $\geq$ c , if $p_{2}$ = c

用自然语言解释一下，首先我们要理解两个点，第一个是c代表的边际成本点，第二个是 $p_{monopoly}$ 代表的垄断价格点。

第一种情况，当对手的价格低于c时，说明此时卖一件亏一件，所以理性的做法是退出市场止损，而依据假设条件，我们只要价格比对手高，我们就相当于产量归零，退出市场了；

第二种情况，当对手价格小于等于垄断价格，大于c时，这个时候很好理解，有利润，那么我只要比对手的价格低一点点，我就可以获得整个市场（ε代表无穷小）；

第三种情况，对手的价格不仅比c高，居然还比垄断价格高，和上一个情况相同的是，我只要比对手低一点点就能获得整个市场，但我不仅仅想要市场，还想要利润最大化，而垄断价格本身代表了利润最大化的点，所以无论对手价格比垄断价格高多少，我们都应该直接选取垄断价格作为此时的策略；

第四种情况，如果对手价格正好等于c，说明此时市场上已经没有任何经济利润，我们可以加入进去，也选择相同的价格，大家一起零利润过日子，或者选一个高于对手的价格，形成己方实际上退出市场的局面。

根据双方的BR，我们可以发现，当两家公司都选取等于边际成本的价格时，达成纳什均衡。

会不会有别的纳什均衡呢？

依据第四种情况，当对手都不赚钱了，那我选一个高一点点的价格退出市场不也是最优反应么？

这不是均衡，假如 $p_{2}$ = c 时， $p_{1}$ = c + ε，这时2号公司就会有提价的激励，可以将 $p'_{2}$ = c + ε/2，这样就可以赚到经济利润，而1号公司看到这个情况，会有改变价格的激励，可将 $p'_{1}$ = c + ε/4，这样也可以转到经济利润。接下来双方开始继续套娃，直到最后回到 $p_{1}$ = $p_{2}$ = c的纳什均衡点上来。

按照伯川德模型的假设，我们得出了一个和现实市场不太吻合的结论，既在一个双寡头的市场，最终价格等于边际成本，经济利润为零，消费者剩余最大化，和完全竞争市场达成的效果一模一样。

进一步思考，古诺模型和伯川德模型的假设条件几乎是一样的，最大的区别是两个模型中可选的策略不同，仅此一项变化就带来了结果的巨大区别，这多少令人有些疑惑。

为了使得模型能够更好的反应现实，我们就需要进行调整，如，要是产品不是同质化的呢？

2.6* 线性城市模型 Linear City Model

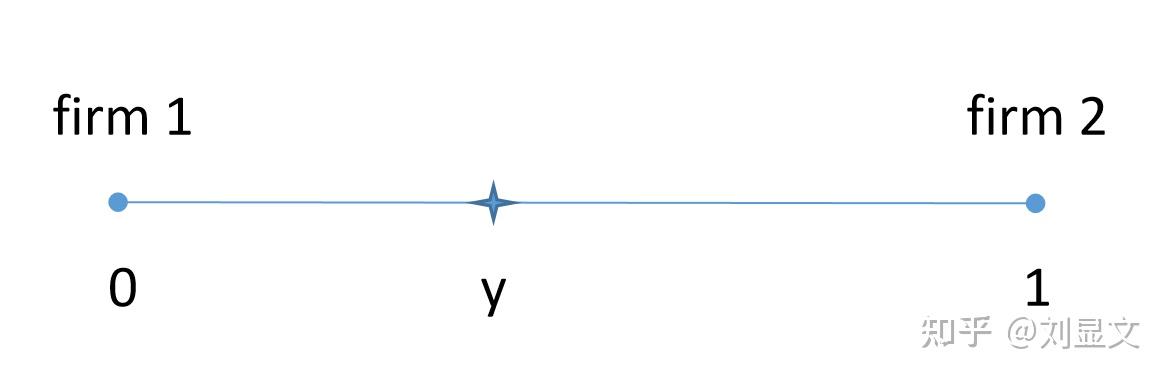
假定有两家公司，相聚彼此相距1公里，他们的消费者均匀的分布在这1公里的范围内，所有消费者会且仅会购买一个产品。以某个特定的消费者y为例，他所在的点距离左边的公司为y，距离右边的公司为1-y，他想 $\geq$ $\geq$ 要购买对自己来说总成本最小的产品，总成本由产品价格p和来回交通费用 $ty^{2}$ 构成，如果他从左边公司购买则为 $p_{1}+ty^{2}$ ，若从右边公司购买则为 $p_{2}+t(1-y)^{2}$ 。